同相加法器是一个在模拟电路中常见的运算放大器（Operational Amplifier, 简称Op-Amp）电路配置，也称为同相求和放大器（Inverting Summing Amplifier）。该电路的主要作用是将多个输入信号按一定比例进行加法运算，并输出一个加权和。由于它使用同相输入端，因此称为“同相”加法器。下面将详细介绍同相加法器的基本原理、设计方法、应用场景以及其在实际电路中的重要性。

　　一、基本原理

　　同相加法器的核心是运算放大器。运算放大器具有两个输入端：一个是同相输入端（标记为“+”），另一个是反相输入端（标记为“-”）。在同相加法器中，多个输入信号通过电阻连接到同相输入端，而反相输入端则通常接地（或连接到适当的偏置电压）。该电路通过反馈电路（通常是一个反馈电阻）来调节输出电压，使得运算放大器的输入电压差接近于零。

　　1. 同相加法器的电路图

　　基本的同相加法器电路图如下：

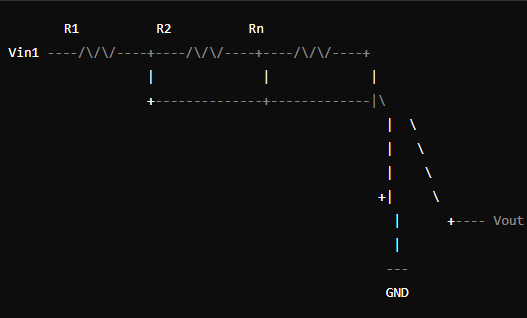
　　在这个电路中，Vin1, Vin2, ..., VinN 是输入信号，R1, R2, ..., Rn 是输入电阻，Rf 是反馈电阻，Vout 是输出信号。

　　2. 输出电压公式

　　在理想情况下，运算放大器的输入电阻是无限大的，输出电阻是零，且具有无限的增益。对于同相加法器，其输出电压 Vout 可以表示为输入信号的加权和，即：

　　Vout=(RfR1⋅Vin1+RfR2⋅Vin2+⋯+RfRn⋅VinN)V_{out} = left( frac{R_f}{R_1} cdot V_{in1} + frac{R_f}{R_2} cdot V_{in2} + cdots + frac{R_f}{R_n} cdot V_{inN} ight)Vout=(R1Rf⋅Vin1+R2Rf⋅Vin2+⋯+RnRf⋅VinN)

　　其中，Rf 是反馈电阻，R1, R2, ..., Rn 是与各个输入信号相连的电阻。

　　二、设计方法

　　设计一个同相加法器时，主要需要考虑以下几个方面：

　　选择适当的电阻值：要确保不同输入信号的加权比例合适，电阻值的选择至关重要。通常，设计者会根据实际应用中的需求来选择合适的电阻值，以达到预期的加权和输出。

　　反馈电阻的选择：反馈电阻 Rf 的选择直接影响输出电压的放大倍数。在大多数情况下，Rf 的选择应与输入电阻成比例，以保证线性放大。

　　考虑运算放大器的特性：运算放大器的选择对于电路的性能至关重要。不同类型的运算放大器具有不同的输入偏置电流、输入失调电压、带宽等参数。这些特性会影响同相加法器的准确性和稳定性。

　　三、应用场景

　　同相加法器广泛应用于各类模拟信号处理场合。以下是一些典型的应用场景：

　　音频信号处理：在音频混合器中，同相加法器用于将多个音频信号混合成一个信号输出，确保多个信号可以以适当的比例叠加。

　　传感器信号的集成：在一些测量系统中，多个传感器的输出信号需要集成到一个信号中进行处理。同相加法器可以将多个传感器的输出进行加权求和，以便于后续信号的处理。

　　滤波器设计：同相加法器在有源滤波器设计中也起到重要作用。通过调整电阻和电容的值，可以设计出各种类型的滤波器，如低通滤波器、高通滤波器等。

　　数据采集系统：在数据采集系统中，同相加法器可以用于对多个输入信号进行预处理，从而简化后续的A/D转换过程。

　　四、实际电路中的挑战

　　尽管同相加法器在理论上相对简单，但在实际应用中可能会遇到一些挑战。这些挑战包括但不限于：

　　偏置电流和失调电压：实际的运算放大器并非理想器件，其输入端会存在一定的偏置电流和失调电压。这些因素会引入误差，影响电路的精度。

　　带宽限制：运算放大器的带宽限制会影响同相加法器的频率响应。在高频信号处理中，必须选择高带宽的运算放大器，否则电路的性能会大打折扣。

　　热噪声和失真：在高精度应用中，电阻和运算放大器本身的热噪声和非线性失真会影响电路的性能。因此，在设计中需要谨慎选择低噪声、高线性的器件。

　　电源噪声：运算放大器的电源噪声也会影响同相加法器的输出稳定性。在一些敏感应用中，需要对电源进行适当的滤波和调节。

　　五、总结

　　同相加法器是模拟电路设计中的基本电路之一，具有广泛的应用价值。通过合理的设计和选择合适的元器件，可以实现高精度的信号加权求和。在实际应用中，设计者需要综合考虑电阻的选择、运算放大器的特性以及噪声等因素，以确保电路的性能达到预期要求。

　　六、深入探讨

　　在更高层次的应用中，同相加法器还可以与其他电路模块结合，形成更为复杂的信号处理系统。例如，在信号调制和解调电路中，同相加法器可以与乘法器和积分器配合，形成幅度调制（AM）和相位调制（PM）电路。

　　此外，随着数字信号处理的普及，同相加法器还可以作为模拟前端，负责将模拟信号进行预处理，再传递给后续的数字处理模块。这种混合信号处理方式在现代通信、音频处理和测量系统中得到了广泛应用。

　　总的来说，同相加法器不仅是一个基础的电路元件，还是一个多功能的信号处理工具，其应用范围远超出简单的加法运算。通过不断的创新和优化，同相加法器将在更多领域展现出其强大的应用潜力。

　　七、同相加法器的数学分析

　　为了更深入地理解同相加法器的工作原理，我们可以从数学角度来分析它的行为。考虑一个具有多个输入的同相加法器，其输入信号为 Vin1,Vin2,…,VinNV_{in1}, V_{in2}, ldots, V_{inN}Vin1,Vin2,…,VinN，输入电阻为 R1,R2,…,RNR_1, R_2, ldots, R_NR1,R2,…,RN，反馈电阻为 RfR_fRf。在理想情况下，运算放大器的输入阻抗是无限大的，因此可以假设流入同相输入端的电流为零。

　　根据运算放大器的虚短（Virtual Short）原理，运放的同相和反相输入端电压相等。因此，同相输入端的电压 V+V_+V+ 等于输出电压 VoutV_{out}Vout 和通过反馈电阻 RfR_fRf 分压后的电压。这个分压关系可以表示为：

　　V+=Vout×RfRf+ReqV_+ = V_{out} imes frac{R_f}{R_f + R_{eq}}V+=Vout×Rf+ReqRf

　　其中 ReqR_{eq}Req 是并联电阻 R1,R2,…,RNR_1, R_2, ldots, R_NR1,R2,…,RN 的等效电阻，定义为：

　　1Req=1R1+1R2+⋯+1RNfrac{1}{R_{eq}} = frac{1}{R_1} + frac{1}{R_2} + cdots + frac{1}{R_N}Req1=R11+R21+⋯+RN1

　　由于同相输入端电流为零，输入信号电压和输入电阻之间的关系也遵循简单的电压分配规则，因此可以得出：

　　V+=Vin1R1+Vin2R2+⋯+VinNRNV_+ = frac{V_{in1}}{R_1} + frac{V_{in2}}{R_2} + cdots + frac{V_{inN}}{R_N}V+=R1Vin1+R2Vin2+⋯+RNVinN

　　将这两个方程结合起来，我们可以得到输出电压 VoutV_{out}Vout 的表达式：

　　Vout=(RfR1⋅Vin1+RfR2⋅Vin2+⋯+RfRN⋅VinN)V_{out} = left( frac{R_f}{R_1} cdot V_{in1} + frac{R_f}{R_2} cdot V_{in2} + cdots + frac{R_f}{R_N} cdot V_{inN} ight)Vout=(R1Rf⋅Vin1+R2Rf⋅Vin2+⋯+RNRf⋅VinN)

　　这个公式展示了同相加法器的核心特性：输出电压是各个输入信号按比例（由输入电阻和反馈电阻决定）加权后的和。

　　八、同相加法器与反相加法器的比较

　　在运算放大器电路中，除了同相加法器，反相加法器也是一种常见的加法电路配置。两者的主要区别在于输入信号的位置和输出信号的极性。下面从几个方面来比较这两种电路：

　　1. 电路配置

　　同相加法器：输入信号通过输入电阻连接到运算放大器的同相输入端，反馈电阻连接在输出端和同相输入端之间。输出信号与输入信号同相。

　　反相加法器：输入信号通过输入电阻连接到运算放大器的反相输入端，反馈电阻连接在输出端和反相输入端之间。同相输入端通常接地。输出信号与输入信号反相。

　　2. 增益特性

　　同相加法器：增益由反馈电阻和输入电阻的比例决定。由于输入信号和输出信号同相，适用于要求信号极性保持不变的应用场合。

　　反相加法器：增益同样由反馈电阻和输入电阻的比例决定，但输出信号的极性与输入信号相反。在某些应用中，如信号反转和负反馈控制，反相加法器更具优势。

　　3. 输入阻抗

　　同相加法器：由于同相输入端具有高输入阻抗，因此电路对信号源的负载效应较小。这使得同相加法器更适合与高阻抗信号源连接。

　　反相加法器：反相输入端的输入阻抗由输入电阻决定，通常较低。这意味着电路可能会对信号源产生更大的负载效应。

　　九、实际应用中的考虑因素

　　在实际应用中，设计同相加法器时需要考虑以下几个重要因素：

　　1. 电源噪声与电源退耦

　　运算放大器的电源噪声可能会直接影响到输出信号的质量。因此，必须对运放的电源进行适当的退耦处理，以减少电源噪声对电路性能的影响。常见的退耦方法包括在电源引脚和地之间添加电容器，以滤除高频噪声。

　　2. 温度漂移与电阻匹配

　　运放电路中的电阻会随着温度的变化而产生漂移，导致增益不稳定。在高精度应用中，可以选择温度系数较低的精密电阻，或者使用电阻网络来保证电阻的匹配度。此外，运放的失调电压也会随温度变化，这一点在高精度应用中也需要特别注意。

　　3. 带宽与稳定性

　　在设计同相加法器时，电路的带宽和稳定性也是关键因素。运算放大器的带宽决定了电路能够处理的信号频率范围，而过高的增益可能会导致电路的不稳定性，如振荡或过冲。为确保电路的稳定性，设计者可以通过引入补偿电容或者选择带宽较宽的运算放大器来解决这些问题。

　　4. 噪声与失真

　　同相加法器电路中的噪声源主要包括运算放大器的本底噪声、输入电阻的热噪声以及电源噪声等。在设计过程中，需要选择低噪声的元器件，并优化电路布局以最小化噪声的影响。此外，运算放大器的非线性失真也可能导致信号失真，特别是在高频或大信号幅度时。因此，在高保真音频或精密测量应用中，这些因素需要仔细考虑。

　　十、进阶设计：多功能同相加法器

　　在实际应用中，同相加法器可以结合其他电路模块，设计出具有更多功能的电路。例如，通过结合滤波器、整流电路或非线性元件，可以构建出具备信号调制、整流、峰值检测等功能的复杂电路。

　　1. 同相加法器与滤波器结合

　　将同相加法器与有源滤波器结合，可以实现加权求和与滤波的双重功能。例如，可以设计一个低通或带通滤波器，同时将多个输入信号进行加权求和。这种电路在音频处理、信号调理和通信系统中具有广泛应用。

　　2. 同相加法器与整流电路结合

　　在信号处理应用中，特别是峰值检测或信号包络提取中，可以将同相加法器与精密整流器结合使用。通过这种设计，可以实现对多个交流信号的加权求和，并提取其包络信号。这在调幅解调和信号分析中尤为有用。

　　3. 同相加法器与非线性元件结合

　　通过在同相加法器中引入非线性元件，如二极管或场效应晶体管（FET），可以设计出非线性加权和电路。这类电路在自适应滤波、信号压缩和动态范围调整中具有重要作用。

　　十一、未来发展方向

　　随着电子技术的发展，同相加法器的设计和应用也在不断进步。未来的发展方向可能包括：

　　1. 更高精度和更低功耗

　　随着运算放大器技术的进步，同相加法器在精度和功耗方面将得到进一步优化。这将有助于在便携式设备和低功耗传感器应用中实现更高性能。

　　2. 集成化与小型化

　　随着集成电路技术的发展，同相加法器电路可能会更多地集成到系统级芯片（SoC）或特定应用芯片（ASIC）中。这将有助于减少电路板面积，提升系统的集成度和可靠性。

　　3. 数模混合设计

　　在现代电子系统中，模拟和数字信号处理往往结合使用。未来，同相加法器可能会更多地与数字信号处理单元结合，形成混合信号处理系统。这将大大增强电路的功能性和灵活性。