由： 马歇尔大脑

　　布尔逻辑会影响计算机的运行方式。 蒙蒂乐森/盖蒂图片社

　　你有没有想过计算机如何做一些事情，比如平衡支票簿，或者 下棋，还是对文档进行拼写检查?这些事情，就在几十年前，只有人类才能做到。现在计算机显然很容易做到。由硅和电线组成的“芯片”如何做一些看似需要人类思考的事情?

　　如果你想从最核心上理解这个问题的答案，你需要理解的第一件事是所谓的 布尔逻辑.布尔逻辑最初由乔治·布尔在 1800 年代中期开发，允许将许多意想不到的东西映射到 位和字节.布尔逻辑的伟大之处在于，一旦你掌握了窍门，布尔逻辑(或者至少是理解计算机操作所需的部分)就非常简单。在本文中，我们将首先讨论简单的逻辑“门”，然后看看如何将它们组合成有用的东西。

　　简易闸门

　　非门

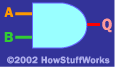
　　和门

　　手术室门

　　诺尔门

　　您需要了解三个，五个或七个简单的门，具体取决于您要如何计算它们(您稍后会明白为什么)。通过这些简单的门，您可以构建组合，实现您能想象到的任何数字组件。这些门在这里看起来有点枯燥，而且非常简单，但我们将在以下部分中看到一些有趣的组合，使它们更加鼓舞人心。如果您还没有这样做，请阅读 位和字节的工作原理 在继续之前会有所帮助。

　　非门

　　最简单的门称为“逆变器”或非门。它接受一个位作为输入，并产生相反的输出。逻辑表为：

　　一问

　　0 1

　　1 0

　　NOT 门有一个输入，称为 一个 和一个输出称为 Q (“Q”用于输出，因为如果您使用“O”，则很容易将其与零混淆)。下表显示了门的行为方式。将 0 应用于 A 时，Q 将生成 1。将 1 应用于 A 时，Q 会产生 0。简单。

　　和门

　　AND 门对两个输入 A 和 B 执行逻辑“和”操作：

　　阿 乙 问

　　0 0 0

　　0 1 0

　　1 0 0

　　1 1 1

　　AND门背后的想法是，“如果 和 B 都是 1，那么 Q 应该是 1。 您可以在门的逻辑表中看到该行为。您逐行阅读此表，如下所示：

　　阿 乙 问

　　0 0 0 如果 A 为 0，B 为 0，则 Q 为 0。

　　0 1 0 如果 A 为 0，B 为 1，则 Q 为 0。

　　1 0 0 如果 A 为 1，B 为 0，则 Q 为 0.

　　1 1 1 如果 A 为 1，B 为 1，则 Q 为 1。

　　手术室门

　　下一个门是 OR 门。它的基本思想是，“如果 A 是 1 或 B 是 1(或两者都是 1)，那么 Q 是 1。

　　阿 乙 问

　　0 0 0

　　0 1 1

　　1 0 1

　　1 1 1

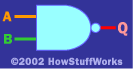
　　南门

　　这是三个基本的门(这是计算它们的一种方法)。识别另外两个也是很常见的： 非南 和 也不 门。这两个门只是 AND 或 OR 门与 NOT 门的组合。如果包括这两个门，则计数上升到五个。以下是 NAND 和 NOR 门的基本操作 - 您可以看到它们只是 AND 和 OR 门的反转：

　　诺尔门

　　阿 乙 问

　　0 0 1

　　0 1 0

　　1 0 0

　　1 1 0

　　南门

　　阿 乙 问

　　0 0 1

　　0 1 1

　　1 0 1

　　1 1 0

　　有时添加到列表中的最后两个门是 异或 和 XNOR 门，也称为“独占”和“独占”非“门。以下是他们的表格：

　　异或门

　　阿 乙 问

　　0 0 0

　　0 1 1

　　1 0 1

　　1 1 0

　　XNOR门

　　阿 乙 问

　　0 0 1

　　0 1 0

　　1 0 0

　　1 1 1

　　异或门

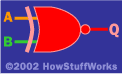
　　XNOR门

　　异或门背后的想法是，“如果 或 B 是 1，但 不 两者都是，Q 是 1。 XOR 可能不包含在门列表中的原因是，您可以使用列出的原始三个门轻松实现它。

　　如果您尝试 A 和 B 的所有四种不同模式并通过电路跟踪它们，您会发现 Q 的行为类似于 XOR 门。由于异或门有一个很好理解的符号，因此通常更容易将异或视为“标准门”，并以与电路图中的AND和OR相同的方式使用它。

　　简单的加法器

　　在关于 位和字节，您了解了 二进制加法.在本节中，您将学习如何使用上一节中描述的门创建能够进行二进制加法的电路。

　　让我们从一个 单比特加法器.假设您有一个项目，您需要将单个位相加并获得答案。您开始为此设计电路的方式是首先查看所有逻辑组合。您可以通过查看以下四个总和来做到这一点：

　　0 + 0 = 0

　　0 + 1 = 1

　　1 + 0 = 1

　　1 + 1 = 10

　　在你达到 1 + 1 之前，这看起来很好。在这种情况下，你有那个讨厌的 进位 要担心。如果你不关心携带(因为这毕竟是一个 1 位加法问题)，那么你可以看到你可以用 XOR 门解决这个问题。但是，如果您确实关心，那么您可以重写您的方程式以始终包含 2 位输出喜欢这个：

　　0 + 0 = 00

　　0 + 1 = 01

　　1 + 0 = 01

　　1 + 1 = 10

　　从这些等式中，您可以形成逻辑表：

　　带外带的 1 位加法器

　　A B Q CO

　　0 0 0 0

　　0 1 1 0

　　1 0 1 0

　　1 1 0 1

　　通过查看此表，您可以看到可以使用 XOR 门实现 Q，并使用 AND 门实现 CO(带出)。简单。

　　如果要将两个 8 位字节加在一起怎么办?这变得稍微困难一些。最简单的解决方案是将问题模块化为 可重复使用的组件 然后复制组件。在这种情况下，我们只需要创建一个组件：a 全二进制加法器.

　　完整加法器和我们之前查看的加法器之间的区别在于，完整加法器接受 A 和 B 输入以及 随身携带 (CI)输入。一旦我们有一个完整的加法器，那么我们可以将其中的八个串在一起以创建一个字节宽的加法器，并将进位从一个加法器级联到下一个加法器。

　　在下一节中，我们将了解如何在电路中实现完整的加法器。

　　全加法器

　　完整加法器的逻辑表比我们以前使用的表稍微复杂一些，因为现在我们有 3 个输入位.它看起来像这样：

　　具有随身携带和带出功能的一位全加法器

　　CI A B Q CO

　　0 0 0 0 0

　　0 0 1 1 0

　　0 1 0 1 0

　　0 1 1 0 1

　　1 0 0 1 0

　　1 0 1 0 1

　　1 1 0 0 1

　　1 1 1 1 1

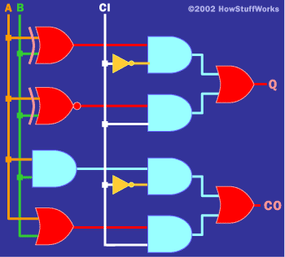
　　Full adders can be implemented in a wide variety of ways.

　　There are many different ways that you might implement this table. I am going to present one method here that has the benefit of being easy to understand. If you look at the Q bit, you can see that the top 4 bits are behaving like an XOR gate with respect to A and B, while the bottom 4 bits are behaving like an XNOR gate with respect to A and B. Similarly, the top 4 bits of CO are behaving like an AND gate with respect to A and B, and the bottom 4 bits behave like an OR gate. Taking those facts, the following circuit implements a full adder:

　　这绝对不是实现完整加法器的最有效方法，但使用此方法非常容易理解和跟踪逻辑。如果你有这样的倾向，看看你可以做些什么来用更少的门来实现这个逻辑。

　　现在我们有了一个叫做“完整加法器”的功能。然后，计算机工程师所做的就是“黑匣子”，这样他或她就可以不再担心组件的细节。一个 黑盒子 对于完整的加法器，如下所示：

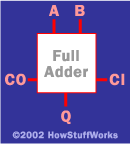
　　有了这个黑匣子，现在很容易画一个 4 位全加法器:

　　在此图中，每个位的进展直接馈入下一个位的进料。0 硬连接到初始进位。如果您在 A 和 B 行上输入两个 4 位数字，您将在 Q 行上得到 4 位总和，加上 1 个额外的位用于最终结转。您可以看到，如果需要，该链可以扩展到8，16或32位。

　　我们刚刚创建的 4 位加法器称为 纹波型进位 蝰蛇。它之所以得名，是因为进位从一个加法器到下一个加法器“纹波”。这种实现的优点是简单，但缺点是速度问题。在实际电路中，门需要时间来切换状态(时间在纳秒量级，但在高速计算机中，纳秒很重要)。因此，由于进位纹波，32 位或 64 位纹波加法器可能需要 100 到 200 纳秒才能稳定到其最终总和。出于这个原因，工程师们创造了更先进的加法器，称为 前瞻 加法 器。实现前进位所需的门数很多，但加法器的建立时间要好得多。

　　人字拖

　　使用两个逆变器的最简单反馈电路你可以用布尔门做的一件更有趣的事情是创建 记忆 和他们在一起。如果正确排列门，它们将记住输入值。这个简单的概念是 公羊 (随机存取存储器)在计算机中，并且还可以创建各种其他有用的电路。

　　记忆依赖于一个叫做 反馈.也就是说，门的输出被反馈到输入中。使用两个逆变器的最简单反馈电路如上所示。

　　如果遵循反馈路径，您可以看到，如果 Q 恰好为 1，它将始终为 1。如果恰好为 0，则始终为 0。由于能够控制我们创建的电路很好，所以这个电路没有多大用处 - 但它确实可以让您看到反馈的工作原理。

　　事实证明，在“真实”电路中，您实际上可以使用这种简单的逆变器反馈方法。一个更有用的 使用两个NAND门的反馈电路如下所示：

　　该电路有两个输入(R 和 S) 和两个输出 (Q 和 Q').由于反馈，与我们之前看到的逻辑表相比，它的逻辑表有点不寻常：

　　R S Q Q'

　　0 0 非法

　　0 1 1 0

　　1 0 0 1

　　1 1 记住

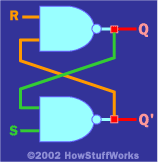
　　逻辑表显示的是：

　　如果 R 和 S 彼此相反，则 Q 跟随 S，Q' 是 Q 的逆。

　　如果R和S同时切换到1，则电路 记得 之前在 R 和 S 上介绍的内容。

　　还有搞笑的 非法 州。在这种状态下，R 和 S 都变为 0，这在内存意义上没有值。由于非法状态，您通常会添加一点 调节逻辑 在输入侧防止它，一个此处显示：

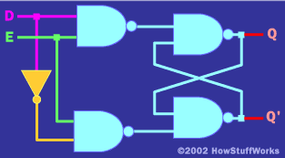
　　在该电路中，有两个输入(D和E)。你可以想到 D 作为“数据”和 E 如果 E 为 1，则 Q 将跟随 D。但是，如果 E 更改为 0，Q 将记住上次在 D 上看到的内容。以这种方式运行的电路通常称为 人字拖.

　　在下一节中，我们将介绍 J-K 触发器。

　　J-K 人字拖

　　一种非常常见的人字拖形式是 J-K 人字拖.从历史上看，目前尚不清楚“J-K”这个名字是从哪里来的，但它通常用这样的黑匣子表示：

　　在此图中， P 代表“预设”， C 代表“清除”和 时钟 代表“时钟”。

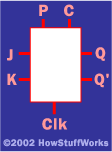
　　J-K 触发器可用于创建和边缘触发锁存，这对 CPU 的设计非常重要。

　　P C Clk J K Q Q'

　　1 1 1 比 0 1 0 1 0

　　1 1 1 比 0 0 1 0 1

　　1 1 1 1 比 0 1 1 切换

　　1 0 x x x 0 1

　　0 1 x x 1 0

　　下表是这样说的：首先，预设和清除完全覆盖 J、K 和 Clk。因此，如果预设变为 0，则 Q 变为 1;如果 Clear 变为 0，则无论 J、K 和 Clk 在做什么，Q 都会变为 0。但是，如果预设和清除均为 1，则 J、K 和 Clk 可以操作。这 1对0 符号意味着当时钟从 1 变为 0 时，如果 J 和 K 的值相反，则会记住它们。在 低边 的时钟(从 1 到 0 的转换)，存储 J 和 K。但是，如果 J 和 K 恰好在低边为 1，则 Q 只是 切换.也就是说，Q 从其当前状态变为相反状态。

　　你现在可能会问自己，“这到底有什么好处? 事实证明，”边缘触发“的概念非常有用。事实上，J-K 触发器仅在从 1 到 0 的转换中“锁存”J-K 输入，这使得它作为存储设备更有用。J-K 人字拖在 计数器 (在以下情况下广泛使用 创建数字时钟).下面是一个示例 使用 J-K 触发器的 4 位计数器:

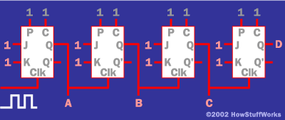
　　该电路的输出为A、B、C和D，它们代表一个4位二进制数。在最左边的人字拖的时钟输入中，有一个信号反复从 1 变为 0，然后又变回 1(一个 振荡信号).计数器将计算它在此信号中看到的低边沿。也就是说，每次输入信号从 1 变为 0 时，由 A、B、C 和 D 表示的 4 位数字将递增 1。因此，计数将从 0 变为 15，然后循环回 0。您可以向此计数器添加任意数量的位，并计算您喜欢的任何内容。例如，如果您在门上放置磁性开关，计数器将计算门打开和关闭的次数。如果你在道路上放置一个光学传感器，计数器可以计算驶过的汽车数量。

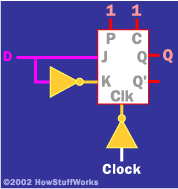
　　J-K 触发器的另一个用途是创建一个 边缘触发锁存器，如下所示。

　　在这种安排中，当时钟边沿从低到高时，D上的值被“锁存”。 锁 存 在诸如以下事物的设计中非常重要 中央处理单元 计算机中的(CPU)和外围设备。

　　实施门

　　在前面的部分中，我们看到，通过使用非常简单的布尔门，我们可以实现加法器、计数器、锁存器等。这是一个巨大的成就，因为不久前，人类是唯一能够做到将两个数字相加的人。只要稍加努力，就不难设计出实现减法、乘法、除法的布尔电路......您可以看到，我们离袖珍计算器并不遥远。从那里开始，跳到全面发展并不太远 中央处理器 用于计算机。

　　那么我们如何在现实生活中实现这些门呢?布尔先生把它们写在纸上，在纸上看起来很棒。然而，要使用它们，我们需要在物理现实中实现它们，以便门可以主动执行它们的逻辑。一旦我们实现了这一飞跃，那么我们就开始了创建真正计算设备的道路。

　　理解布尔逻辑的物理实现的最简单方法是使用 继 电器.事实上，这就是第一台计算机的实现方式。没有人再用继电器实现计算机了——今天，人们使用蚀刻在硅芯片上的亚微观晶体管。这些晶体管非常小且速度快，与继电器相比，它们消耗的功率非常少。然而，继电器非常容易理解，它们可以非常简单地实现布尔逻辑。由于这种简单性，您将能够看到从“纸上的门”到“在物理现实中实现的活动门”的映射是可能且直接的。使用晶体管执行相同的映射同样简单。

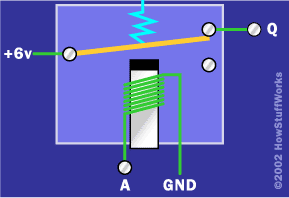
　　让我们从逆变器开始。使用继电器实现NOT门很容易：我们要做的是使用电压来表示位状态。我们将二进制 1 定义为 6 伏，将二进制 0 定义为零伏(接地)。然后我们将使用 6 伏 电池 为我们的电路供电。因此，我们的 NOT 门将如下所示：

　　[如果这个数字对你来说没有意义，请阅读 继电器的工作原理 解释一下。

　　在这个电路中，你可以看到，如果你对A施加零伏特，那么你在Q上得到6伏特;如果你对 A 施加 6 伏特，你会在 Q 上得到零伏特。实现带继电器的逆变器非常容易!

　　实现带有两个继电器的AND门同样容易：

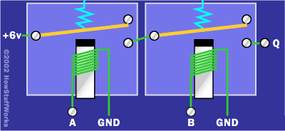
　　在这里你可以看到，如果你对 A 和 B 施加 6 伏，Q 将有 6 伏。否则，Q 的电压为零。这正是我们想要从 AND 门获得的行为。OR门甚至更简单 - 只需将A和B的两根电线连接在一起即可创建OR。如果您愿意并并行使用两个继电器，您可以获得比这更华丽的东西。

　　从这个讨论中可以看出，你可以从继电器创建三个基本门——NOT、AND 和 OR。然后，您可以使用上面显示的逻辑图将这些物理门连接在一起，以创建物理 8 位纹波进位加法器。如果您使用简单的开关将 A 和 B 输入施加到加法器并将所有八条 Q 线连接到灯泡，您将能够将任意两个数字相加并在灯上读取结果(“亮起”= 1，“灯熄灭”= 0)。

　　简单门形式的布尔逻辑非常简单。从简单的门，您可以创建更复杂的功能，例如加法。物理实施门是可能且容易的。从这三个事实中，您拥有数字革命的核心，并且您了解计算机的核心工作原理。